(M1330-05-25) Generalization of the Tabletability Equation for Describing Powder Properties as a Function of Compaction Pressure

Purpose: The recent derivation of a powder tabletability equation [1], which describes tablet tensile strength as a function of compaction pressure, combines the Kuentz-Leuenberger compressibility model [2] with the Ryshkewitch-Duckworth [3,4] exponential compactibility model. A generalization of this model that describes other material properties that are exponentially dependent on porosity, like elastic modulus [5] and hardness [6], as a function of compaction pressure, may facilitate a more comprehensive understanding of powdered materials in powder compaction research. In this work, we apply a generalized version of the tabletability equation (Eq. (1)) to describe elastic and constrained modulus as a function of compaction pressure and extend this to characterizing Poisson’s ratio at zero porosity. In this function, X_max is the asymptotic property as pressure (P) approaches infinity, α_X is a property-dependent constant, β describes powder plasticity equivalently to the tabletability equation, and W is the Lambert W function. Furthermore, we decompose this relationship to describe in-die and out-of-die elastic recovery as a function of compaction pressure. These relationships may have applications in understanding and characterizing material properties critical to predicting tableting issues, like capping and lamination.

X = X_max exp(α_X W(exp(-exp(-P / β - 1)))    (1)

Methods: Compression data for a variety of pharmaceutically relevant materials were obtained from a previous publication [1]. This included microcrystalline cellulose (MCC, Avicel PH102), lactose monohydrate (LM, 316 Fast-flo), dicalcium phosphate anhydrous (DCPA), dicalcium phosphate dihydrate (DCPD), mannitol (Mann, Pearlitol 200SD), urea, ferulic acid (FA), hydroxypropyl cellulose (HPC, EF), and a set of binary mixtures of MCC with DCPA). The tablet elastic (E) and constrained (M) modulus of a tablet made at a given pressure (P) were calculated using Eqs. (2) and (3), respectively, where ER is the fractional elastic recovery.

E = P/ER_out-of-die    (2)

M = P/ER_in-die    (3)

Substituting E and M and for X in Eq. (1) gives a relationship for these modulus values as a function of P. Furthermore, solving Eqs. (2) and (3) for ER_out-of-die and ER_in-die, respectively, gives elastic recovery as a function of P (Eqs. (4) and (5)).

ER_out-of-die = E_max^-1 exp(-α_E W(exp(-exp(-P / β - 1))) P    (4)

ER_in-die = M_max^-1 exp(-α_M W(exp(-exp(-P / β - 1))) P    (5)

Finally, calculating a zero porosity Poisson’s ratio (ν₀) was possible using and E₀ and M₀ for a given material with Eq. (6) [7].

ν₀ = (E₀-M₀+(E₀²+9M₀²-10E₀M₀)^½)/(4M₀)    (6)

Results: Equation (1) shows excellent agreement with experimental data when E_max (Figs. 1a, 1b) and M_max (Figs. 1c, 1d) values were fixed at their zero-porosity equivalents. Comparing the parameters obtained from E and M with those obtained from tabletability data revealed a strong correlation between β parameters (Fig. 2). Although expected due to their mathematical equivalence, the strong correlation is powerful considering that it was obtained from two separate measures. These results shows that β, which is a measure of material plasticity [1], may be obtained from regression of Eq. (1) to other properties, including those obtained from easy-to-collect in-die methods. This is important for fast, efficient materials characterization, which is an essential component to expedited tablet formulation development. Both out-of-die (Figs. 3a, 3b) and in-die (Figs. 3c, 3d) ER data could be well described by Eqs. (4) and (5), respectively, for all materials included in the dataset, including powder mixtures. Elastic recovery, which plays a major role in accurately simulating roller compaction [8] and predicting tablet defects, like lamination, can now be mathematically modeled as a function of P based on constants (E_max, α_E, M_max, α_M, and β) that represent key powder properties. Finally, the calculated ν₀ for MCC (0.370) and Mann (0.306) with Eq. (6) were in reasonable agreement with values obtained using a complementary double compression method using an instrumented die [9,10]. Validation of the ν₀ values for remaining materials is needed, but if proven accurate, this method would be a convenient method for measuring a material or mixture’s ν in the absence of an instrumented die.

Conclusion: We have generalized the tabletability equation to quantitatively model the relationship between any tablet property that exponentially depends on porosity, like the elastic and constrained modulus, and compaction pressure. Using the elastic and constrained modulus, equations were also developed to describe elastic recovery as s function of compaction pressure. Finally, calculation of Poisson’s ratio was made possible using the two moduli, providing a potentially convenient method for measuring important elastic properties of powders in the absence of radial die-wall sensors. These developments may be employed to ultimately help better characterize the compression properties of powdered materials, which is expected to expedite formulation design for tablet products.

References: [1] G. Vreeman, C.C. Sun, A powder tabletability equation, Powder Technol. 408 (2022) 117709.
[2] M. Kuentz, H. Leuenberger, Pressure susceptibility of polymer tablets as a critical property: A modified Heckel equation, J. Pharm. Sci. 88 (1999) 174–179.
[3] E. Ryshkewitch, Compression strength of porous sintered alumina and zirconia, J. Am. Ceram. 36 (1953) 65–68.
[4] W. Duckworth, Discussion of Ryshkewitch paper by Winston Duckworth, J. Am. Ceram. 36 (1953) 68–68.
[5] R.M. Spriggs, Expression for effect of porosity on elastic modulus of polycrystalline refractory materials, particularly aluminum oxide, J. Am. Ceram. 44 (1961) 628–629.
[6] S. Patel, C.C. Sun, Macroindentation hardness measurement—Modernization and applications, Int. J. Pharm. 506 (2016) 262–267.
[7] G. Mavko, T. Mukerji, J. Dvorkin, The Rock Physics Handbook, 3rd ed., Cambridge University Press, 2020.
[8] H.L. Keizer, P. Kleinebudde, Elastic recovery in roll compaction simulation, Int. J. Pharm. 573 (2020) 118810.
[9] V. Mazel, V. Busignies, H. Diarra, P. Tchoreloff, Measurements of elastic moduli of pharmaceutical compacts: A new methodology using double compaction on a compaction simulator, J. Pharm. Sci. 101 (2012) 2220–2228.
[10] V. Mazel, V. Busignies, H. Diarra, P. Tchoreloff, On the links between elastic constants and effective elastic behavior of pharmaceutical compacts: Importance of Poisson’s ratio and use of bulk modulus, J. Pharm. Sci. 102 (2013) 4009–4014.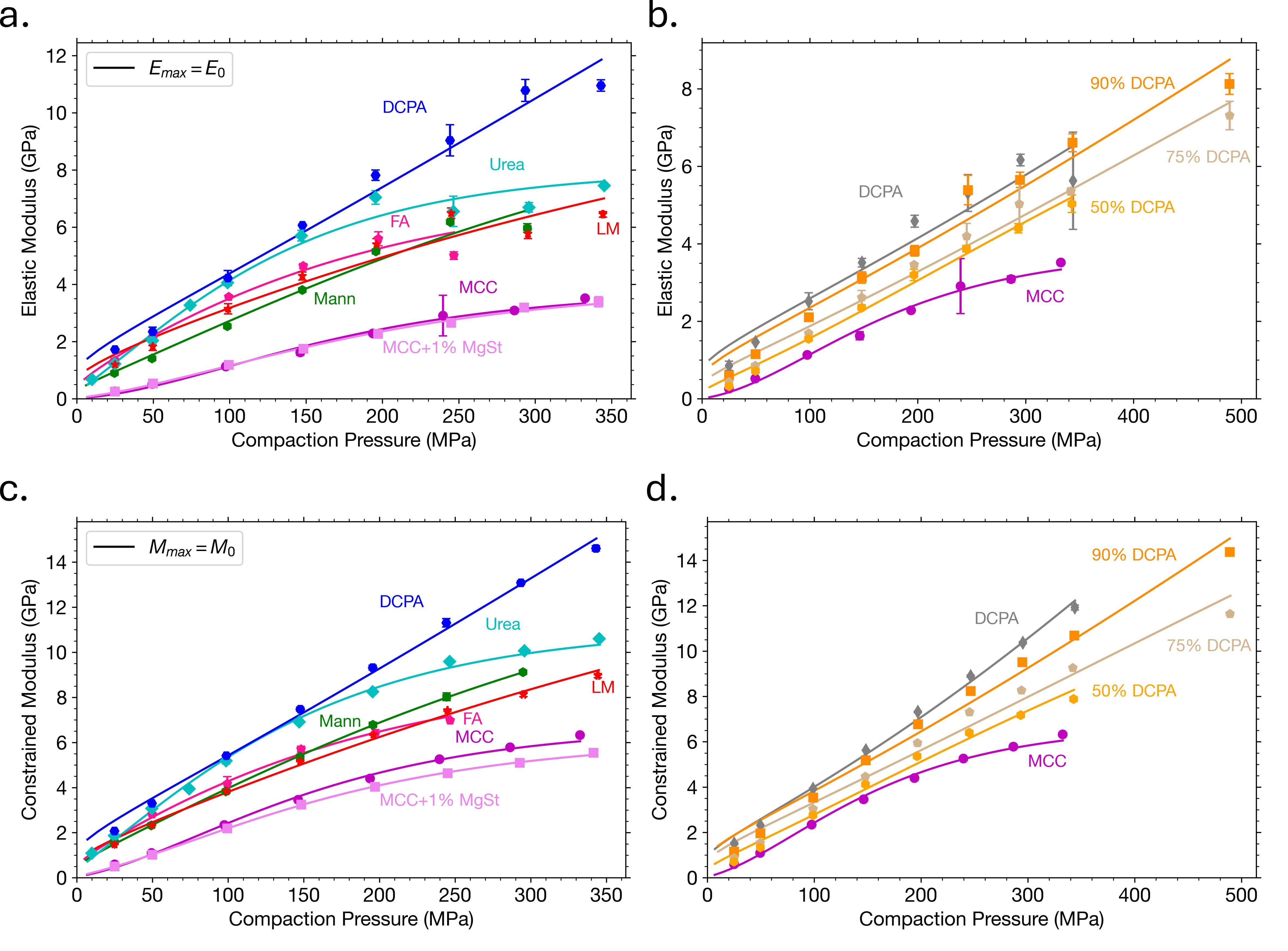


(a, b) Elastic and (c, d) constrained modulus fitted as a function of compaction pressure for (a, c) various pharmaceutically relevant materials and (b, d) mixtures of MCC with DCPA.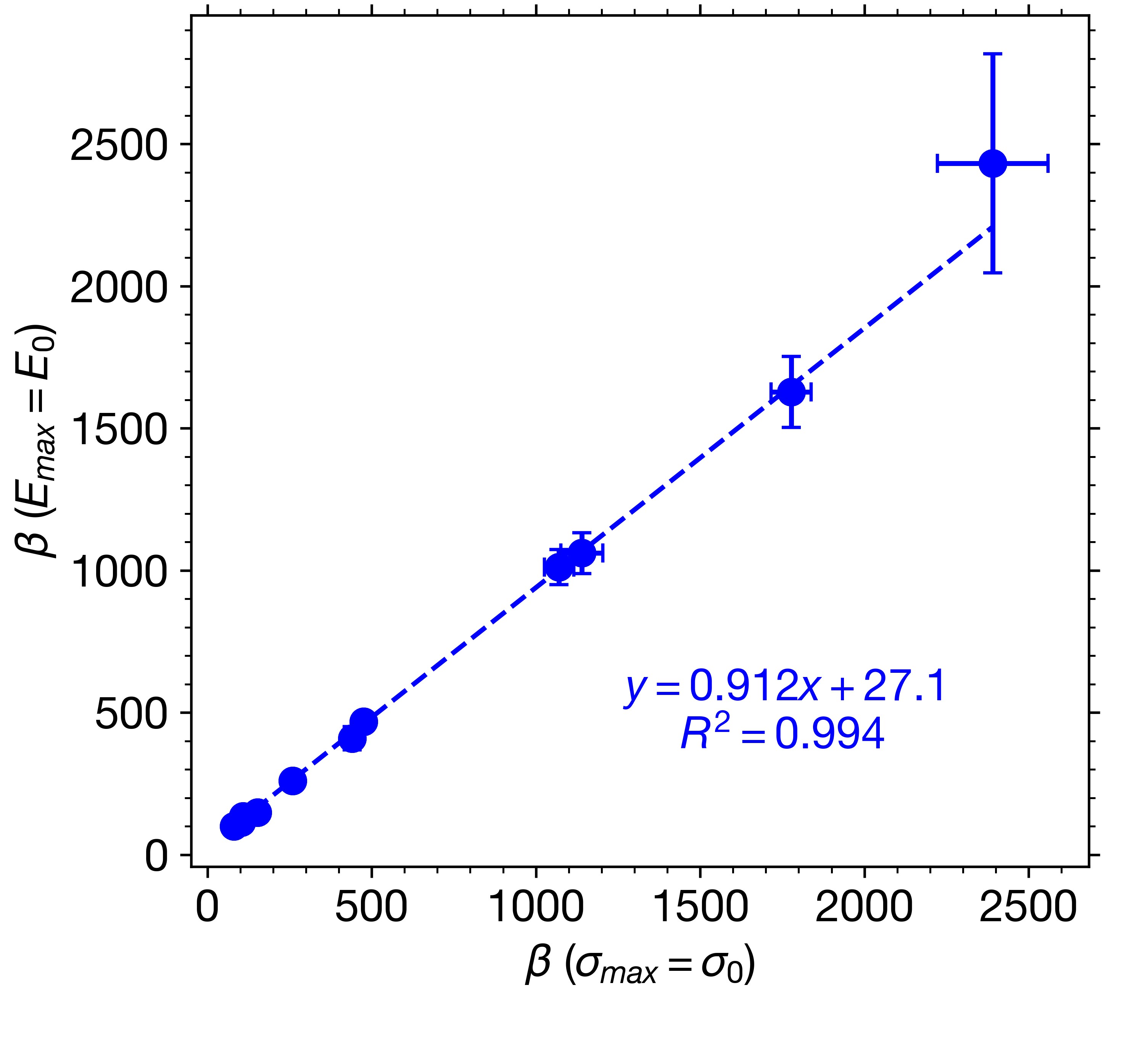


Correlation of β obtained using elastic modulus data versus that obtained using tensile strength data.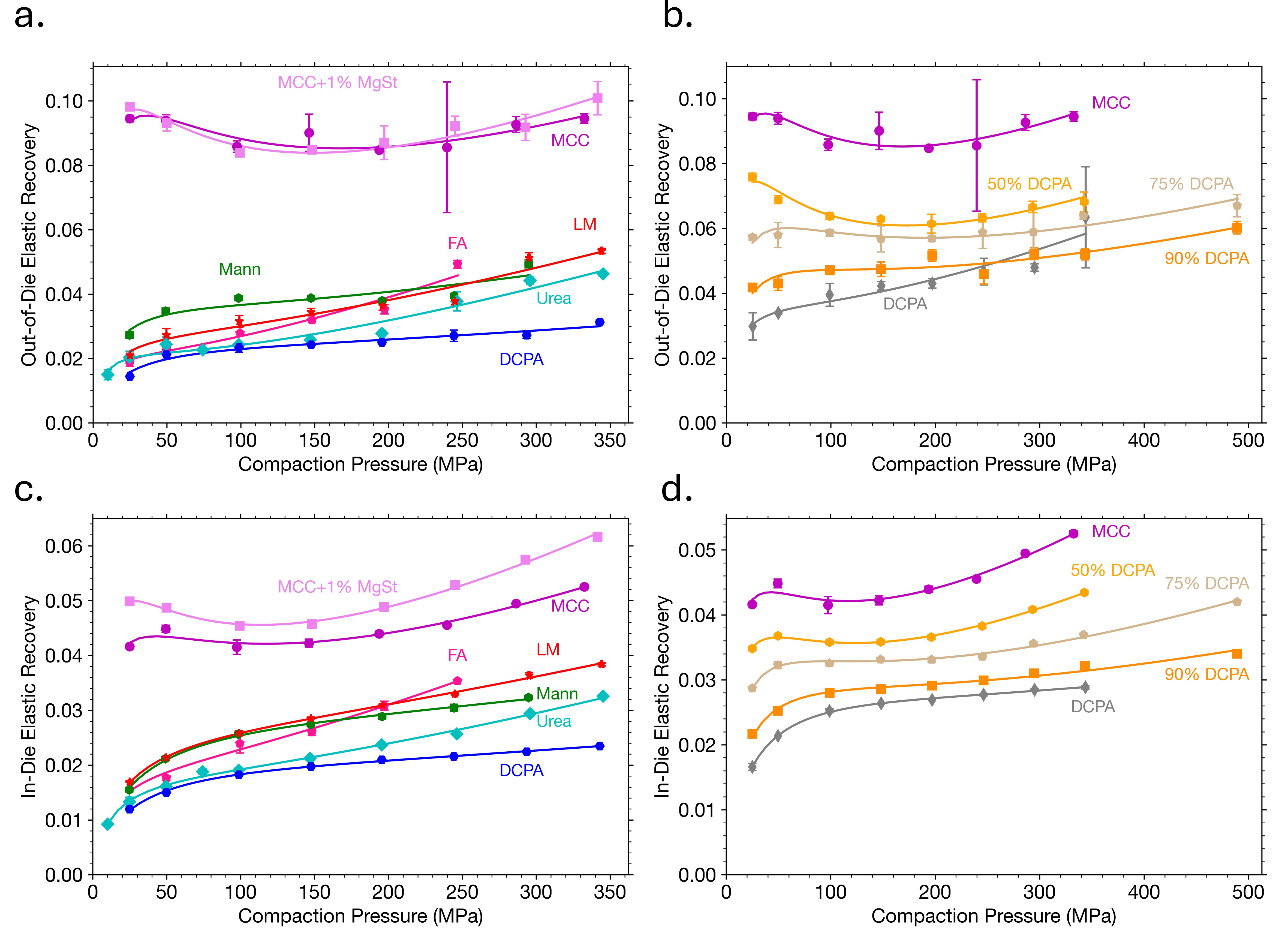


(a, b) Out-of-die and (c, d) in-die elastic recovery fitted as a function of compaction pressure for (a, c) various pharmaceutically relevant materials and (b, d) mixtures of MCC with DCPA.